Brush Gels: Where Theory, Simulations, and Experiments Meet

Abstract
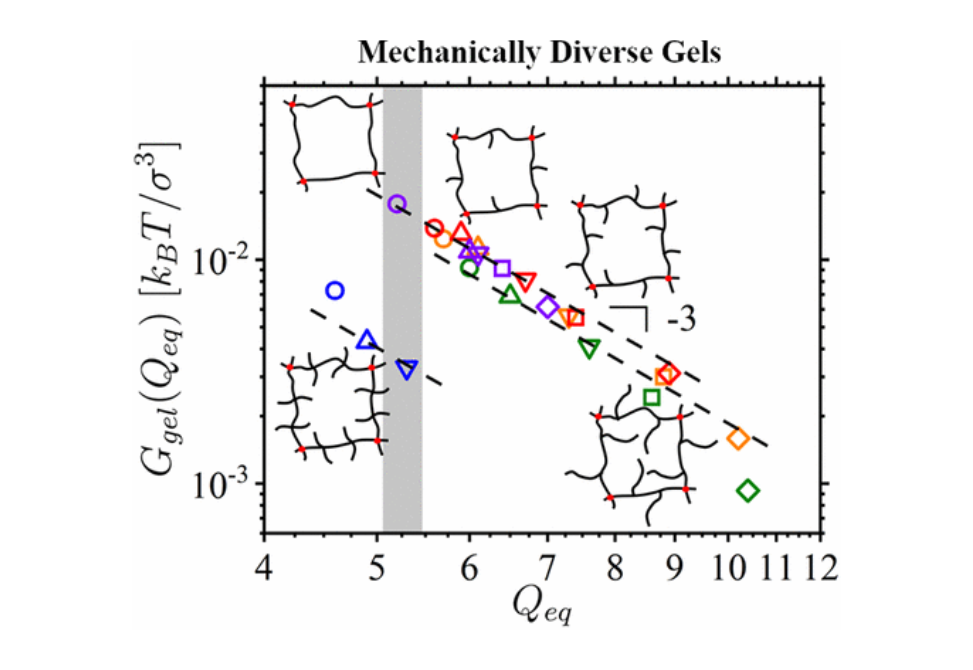
Polymer networks with brush-like (comb or bottlebrush) strands can have mechanical properties similar to biological tissues and can swell to larger volumes than their linear chain counterparts. We use a combination of the Flory–Rehner approach, scaling analysis, molecular dynamics simulations, and experimental data for poly(n-butyl acrylate) (PBA) networks swollen in toluene to elucidate the effect of brush strand architecture on the equilibrium swelling ratio, Q_eq, the modulus of the swollen gel, G_gel(Q_eq), and its relationship with the nonlinear modulus of the dry network, G(Q_eq). Analysis of simulation data and experimental results for PBA gels demonstrates that the gel shear modulus monotonically decreases with increasing equilibrium swelling ratio as G_gel(Q_eq) ∝ Q_eq^–3, which is consistent with a θ-solvent-like swelling behavior. There is a significant effect of the degree of polymerization n_sc and grafting density 1/n_g of the side chains on the gel modulus that manifests as mechanically diverse gels with the same solvent content. This unique behavior is explained by the architecture-controlled stiffening of the brush strands due to the swelling of the side chains in the gel state. In the framework of a scaling model, the effective Kuhn length of the swollen strands, b_K,s, can be expressed in terms of the Kuhn length in the dry state, b_K, and the ratio of shear modulus calculated in the framework of the Flory–Rehner approach, G_gel^FR(Q_eq) = G(Q_eq)/Q_eq^1/3, to the gel modulus G_gel(Q_eq) such that b_K,s ≈ b_KG_gel^FR(Q_eq)/G_gel(Q_eq). The Kuhn length obtained from this analysis highlights different mechanisms of swollen brush rigidity.

Citation
Brush Gels: Where Theory, Simulations, and Experiments Meet Michael Jacobs, Foad Vashahi, Mitchell Maw, Sergei S. Sheiko, and Andrey V. Dobrynin Macromolecules 2022 55 (17), 7922-7931 DOI: 10.1021/acs.macromol.2c01149