Stochastic distinguishability of Markovian trajectories

Abstract
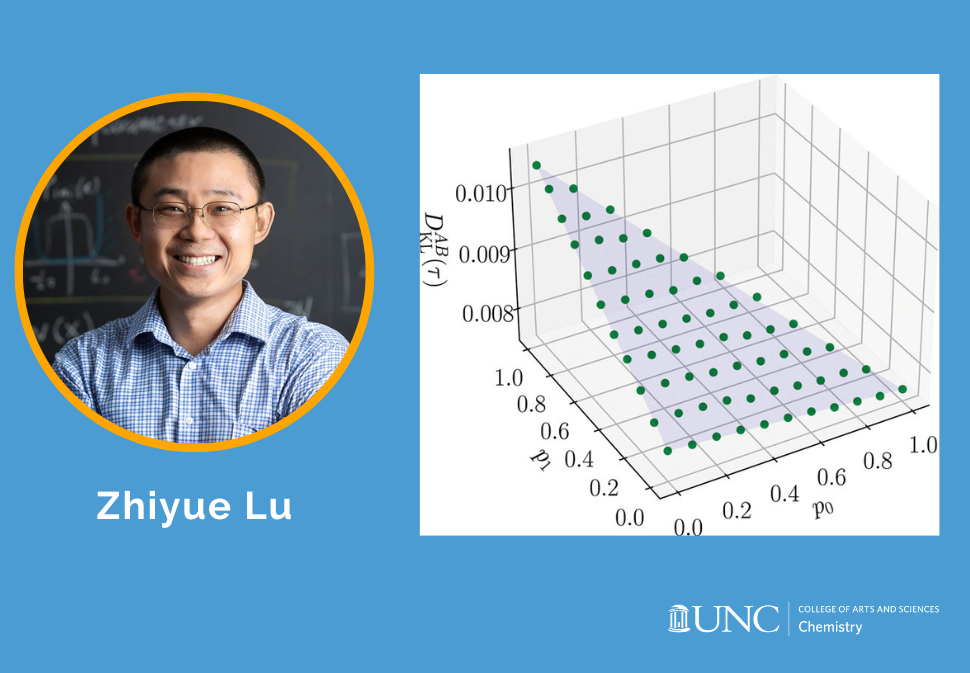
The ability to distinguish between stochastic systems based on their trajectories is crucial in thermodynamics, chemistry, and biophysics. The Kullback–Leibler (KL) divergence, ⁠, quantifies the distinguishability between the two ensembles of length-τ trajectories from Markov processes A and B. However, evaluating from histograms of trajectories faces sufficient sampling difficulties, and no theory explicitly reveals what dynamical features contribute to the distinguishability. This work provides a general formula that decomposes in space and time for any Markov processes, arbitrarily far from equilibrium or steady state. It circumvents the sampling difficulty of evaluating ⁠. Furthermore, it explicitly connects trajectory KL divergence with individual transition events and their waiting time statistics. The results provide insights into understanding distinguishability between Markov processes, leading to new theoretical frameworks for designing biological sensors and optimizing signal transduction.

Citation